BIOCHEMISTRY TOPICS
Entropy
Entropy (S), a state function definable in classical and statistical thermodynamics. Qualitative assessment of entropy changes. ΔS for isothermal expansion of an ideal gas. Engines and entropy.
In order to account for spontaneity or directionality of processes, the concept of entropy is defined and incorporated into what is known as the second law of thermodynamics. Roughly speaking, entropy (symbolized S) is a quantitative measure of the number of ways that energy can be distributed within a system. Entropy can be defined and measured as a thermodynamic quantity. Furthermore, it can be shown that entropy is a state function. These features of entropy are essential to the formulation of the second law. Spontaneous processes such as the attainment of thermal equilibrium or the mixing of gases or liquids can be shown to result in an increase in total entropy, meaning the entropy of the system plus the entropy of the surroundings (Suniv). Indeed, the statement that in any spontaneous process, ΔSuniv > 0 can be taken as a statement of the second law of thermodynamics.
Entropy, was originally defined in classical thermodynamics, which made no assumptions about the detailed nature of matter. The advent and establishment of atomic theory led to the treatment of the macroscopic systems of classical thermodynamics as enormous collections of nanoscale particles by the method of statistical mechanics. The explicit incorporation of atomic and molecular composition of matter into statistical thermodynamics yields the classical quantity entropy in a quite different, yet ultimately equivalent way. In either case, entropy is a state function, just like energy, enthalpy, or any state variable. Both definitions are shown in the figure below.
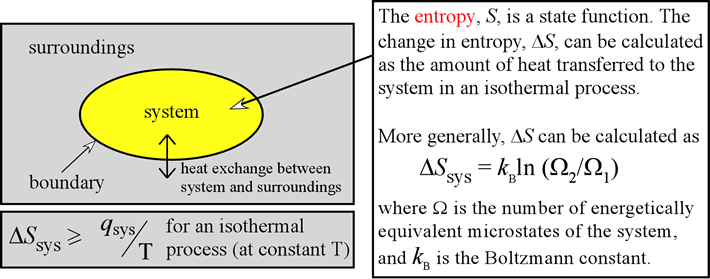
The classical thermodynamic formulation for entropy was originally due to Clausius (1865). This was followed by Boltzmann's statistical thermodynamic approach in 1877.
Understanding entropy
What is entropy? Is entropy "a measure of disorder in a system"? Is the seeming tendency of your room to get messy an example of the inexorable increase in entropy? What is a microstate? Find out the answers to these important questions and many more at this highly recommended Entropy website by Professor Frank Lambert of Occidental College.
Qualitative assessment of entropy changes
We can develop some general rules of thumb for qualitative assessment of entropy changes for various types of processes. First of all, any system that undergoes a process that increases its temperature also increases in entropy; i.e. ΔSsys > 0. This is evident from the classical definition of entropy, since q is positive for any real system undergoing a process in which ΔTsys > 0. Where T is not constant, the classical definition becomes dS = δqrev/ T, which must be integrated in order to obtain ΔSsys for the process. The integral is always non-negative for δq positive, i.e. heat passing into the system from the surroundings. The quantities dS and δqrev are called differentials, and represent an infinitesimal change in entropy and an infinitesimal amount of heat transfer, respectively. (We note in passing for now that although dS and δqrev are both differentials, there is a crucial distinction between them, which corresponds mathematically to the fact that S is a state function, while q is not. This is described further below.)
For a phase change, such as the melting of ice to liquid water, or evaporation of water to water vapor, the change from the more to less condensed phase is always associated with ΔS > 0. For a given substance, the relative change in entropy for the evaporation of a liquid is much greater than that for the melting of the solid. In chemical reactions, the change from more numerous simpler, smaller molecules to fewer, larger and more complex molecules generally represents a decrease in entropy. (Note that this is in spite of the fact that a larger molecule has greater entropy than a small one. The kinetic energy in a system of molecules can be more effectively dispersed by an increase in the number of particles with translational freedom than it can by the increased number of vibrational modes within a coherent collection of the same particles linked by chemical bonds.) In reactions where all reactants and products are gases, the entropy change will be positive in the direction of the reaction that produces more total moles of gas. In reactions occurring in solution, or in reactions of heterogeneous systems, production of a gas will make a significant positive contribution to the overall entropy change for the reaction. If a precipitation reaction occurs, this generally makes a a negative contribution to the entropy of reaction, although in this case we need to be careful to consider the entropic contribution of water molecules released when precipitating ions are desolvated.
Trends in S°T, m values
Looking at trends in standard molar entropies (S°T, m values) confirms a number of qualitative predictions and augments our practical understanding of entropy and the change in entropy associated with various processes.
Phases: solid < liquid < gas
Molar mass: S° values increase with increasing molar mass
Molecular complexity: S° values increase with increasing molecular complexity
Allotropes have distinct S° values
Dissolution: Dispersal of a pure substance into a solvent increases its S° value
Notes on these trends: Allotropes are different forms of elements, e.g. diamond and graphite are carbon allotropes. In considering the dissolution of a solute, the ΔS of the solvent must also be accounted for.
Entropy change for isothermal expansion of an ideal gas
We previously used free expansion of an ideal gas as an example of a spontaneous process. The entropy change for such a process can be calculated, provided we are careful about specifying the path. When 1 mol ideal gas expands into a vacuum to double its original volume, it does so against no external pressure, so the system performs no work. Let us further specify the process begin and end at the same temperature.
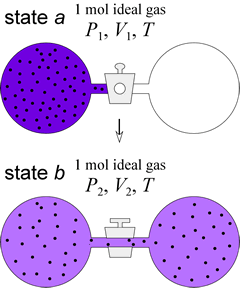
Since the energy of an ideal gas depends only on its temperature, ΔU = 0 for this process. Therefore, q = 0 for the free isothermal expansion of an ideal gas. Does this mean ΔS = 0 for this process? Well, no. The process is irreversible, and qrev ≠ q for this process. What we need to consider is a reversible path for the isothermal expansion, use the formula ΔS = qrev/T to compute ΔS for the reversible process, which will be the same as ΔS for free expansion, since ΔS is a state function and in reversible and irreversible processes, the system has the same beginning and ending states. The process can be carried out reversibly (i.e. along a reversible path) as follows. The boundary of the system is envisioned as a closed cylinder with a movable piston, so that the volume of the system can change continuously. The surroundings, in full thermal contact with the system, are held at a constant temperature T, which maintains the system temperature at T as well.
The initial state of the system is one mol ideal gas at P1, V1, T, while the final state is described as 1 mol ideal gas at P2, V2, T, with P1V1 = P2V2, as required by the ideal gas law. To initiate the process, the external pressure exerted by the piston, Pext, is allowed to decrease infinitesimally below P1 for the system. The system adjusts smoothly to this incremental decrease in Pext , never varying from an equilibrium state, by an infinitesimal increase in volume to allow the pressure to match Pext. The process is reversible, since the direction can be reversed - in this case to compression - by an infinitesimal increase in Pext. We imagine the process moving in the forward direction as this lowering of external pressure continues, and the volume of the system increases, finally reaching V2.
Since V = RT/P for 1 mol ideal gas, we can calculate the work done by the system as the integral of a differential equation derived as follows
qrev = −w = ∫P(V)dV
where P(V)dV = (RT/V)dV . By using this equation, and the fact that T is constant throughout, to write
ΔS = qrev/T = (1/T)∫(RT/V)dV = (RT/T)∫(1/V)dV = R ln(V2 /V1)
where the last equality follows by carrying out the integration from V1 to V2.
Entropy changes for chemical reactions
In cases for which we want to calculate the entropy change ΔS for a given chemical reaction, we follow a procedure similar to that used in calculation of ΔH from standard enthalpies of formation. In this case, we rely on tabulated values of standard entropies (S° values) for all reactant and product species.
Example: Calculate the thermodynamic value ΔS° for the following reaction at 298.15 K (25.00 °C):
N2(g) + 3 H2(g) → 2 NH3(g)
Use the standard entropies given in thermodynamic tables (these are usually found in an appendix of a general chemistry textbook).
Solution: We need the S° values for NH3(g), N2(g), and H2(g). Note that in contrast to the case for standard enthalpies of formation, the S° values for molecular nitrogen gas or diatomic hydrogen gas are not zero. The values are 192.34 J mol−1 K–1 {NH3(g)}, 191.50 J mol–1 K−1 {N2(g)}, and 130.57 J mol−1 K−1 {H2(g)}. To get the standard entropy change for the reaction, multiply the S° values by their stoichiometric coefficients in the chemical equation above (along with the unit "mol"), but using a minus sign for reactants, and then add up all the terms, as shown below:
ΔS° = 2 mol · S°298 {NH3(g)} − 1 mol · S°298 {N2(g)} − 3 mol · S°298{H2(g)}
ΔS°298 = 2 mol ·192.34 J mol−1 K−1 − 1 mol · 191.50 J mol−1 K−1 − 3 mol · 130.57 J mol−1 K−1.
ΔS°298 = − 198.53 J/K
The resulting thermochemical equation is then
N2(g) + 3 H2(g) → 2 NH3(g) ΔS° = − 198.53 J/K
Engines and entropy
The history of the development of the steam engine is not only part of the story about the dawn of the industrial age, but is also intimately associated with the development of classical thermodynamics. The theoretical study of engines led to the definition and measurement of entropy in terms of heat and temperature. The early steam engines were quite inefficient, and there were many attempts to improve them. By the latter half of the 1700s, the Scottish inventor James Watt had made much progress, but even Watt's best engines had an efficiency of only about 5%. Efficiency is defined for an engine by the ratio of amount of input energy - here heat from a fire - to the work output. For a perfect engine, that ratio would be one, or an efficiency of 100%. Now, the first law of thermodynamics says you can't get something for nothing - no engine could ever exceed 100% efficiency - but might someday an engine approaching 100% efficiency be built? In 1824, a Frenchman, Sadi Carnot, published his opus, Reflections on the Motive Power of Fire, that answered this question with a resounding no. Carnot brilliantly showed that the efficiency of even an idealized engine could be no greater than the ratio (Th – Tc) / Th, where Th is the temperature of the hot reservoir, and Tc the temperature of the cold reservoir.

A useful engine must be a device that works in a cyclic mode. Rather than a steam engine, Carnot considered an ideal engine whose working substance was an ideal gas. The high temperature reservoir at temperature Th could theoretically differ from the 373 K of boiling water; similarly, Tc could be other than the lower limit of 273 K for liquid water. The engine operates by the cyclic path shown at left. The paths are reversible paths, meaning they are idealized processes that occur by an infinitesimal displacement from equilibrium, and whose direction of spontaneity can be reversed at any point by an infinitesimal change δq or δw along the path. This idealized heat engine is referred to as the Carnot cycle. The cycle is composed of two isothermal paths, in which T is constant, and two adiabatic paths, for which q = 0, by definition.
Under these conditions, the efficiency can be computed according to the first law:
ΔU = qtot + wtot = qh + qc + wtot = 0 or: – wtot = qh + qc
This says that the total work that can be done by the engine is equal to the heat absorbed from the hot reservoir minus that exhausted to the cold reservoir. This means that efficiency, e, is given by
e = – wtot/ qh = (qh + qc) / qh
Since the two isotherms are joined by two adiabats, it can be shown that
(VD / VC) = (VA/ VB), so that
– wtot = qh + qc = RThln(VB/ VA) – RTcln(VB/ VA) = R ln(VB / VA){Th – Tc}
Thus, efficiency can be expressed as
e = – wtot/ qh = {R ln(VB/ VA)}{Th –Tc}/ RThln(VB/ VA) = (Th –Tc) / Th
Exercise: Show that equating the two above expressions for efficiency e of a heat engine leads to the relation
{ qh / Th } + { qc / Tc } = 0
for the Carnot cycle, suggesting that the quantity qrev/T provides the basis for the definition of a state function (where qrev is the heat transferred to the system along a reversible path.
Clausius was the first to define entropy in the classical sense, which he did after realizing what we showed in the exercise above, and he defined entropy as ΔS = qrev/T (or the integral of dqrev/T for a process in which temperature is changing). This definition is a really a way to compute entropy for an isothermal process, since qrev/T - the heat transferred to the system in a reversible process divided by the temperature at which it occurs - is a state function, whereas q is not. But no matter how we carry out a change in state, ΔS is the same for the same change in state, or (equivalently) ΔS is zero for a cyclic process. In all irreversible (= not reversible = spontaneous) processes, q is not a state function, and is path-dependent, and we can show that ΔSuniv > 0. Mathematically, this means that the integral of a differential quantity of energy transfer as heat, dq, is not uniquely defined as Δq. Actually, we never write Δq or dq for just this reason. The integral of dq is path dependent, and mathematicians have a more succinct way of describing this by saying dq is not an exact differential (and the notation δq is often used to signify this, whereas dU, dH, dS, etc. are all exact differentials).
Related topics pages: