BIOCHEMISTRY TOPICS
Problems in acid-base chemistry
Titrations
Problem 10-9. (ECA5, p.228)
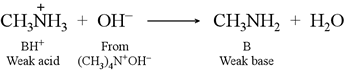
When methylammonium chloride is titrated with tetramethylammonium hydroxide, the titration reaction is as shown at right
Find the equivalence volume in the titration of 25.0 mL of 0.0100 M methylammonium chloride with 0.0500 M tetramethylammonium hydroxide. Calculate the pH at Vb = 0, 2.50, 5.00, and 10.00 mL. Sketch the titration curve.
Solution: At the outset, before the titration begins (Vb = 0), we have a solution of a weak acid with known concentration and a given pKa. Thus the pH is governed by a weak acid equilibrium. Since the formal concentration F of weak acid BH+ is 0.0100 M and pKa = 10.645, we can calculate pH according to our established method:
Ka = 10−10.645 = 2.26 × 10−11
[H+] ≈ √ FKa = (0.0100 · 10−10.645)½ = ( 2.2646443 × 10−13) ½ = 4.7588 × 10−7
pH = −log(4.7588 × 10−7) = 6.3225
Note that this is a very weak acid, and also that by solving the quadratic equation in this case yields
[H+] = 4.7587 × 10−7 and pH = 6.3225
so the error in using the approximate formula for the weak acid pH calculation is in this case truly negligible.
Now before analyzing the titration, let's calculate the equivalence volume:
mmol BH+ = (25.00 mL)(0.01000 mmol/mL) = 0.2500 mmol
Ve = (canalyte· Vanalyte ) / ctitrant = (25.00 mL)(0.01000 mmol/mL) / ( 0.0500 mmol/mL) = 5.000 mL.
We can conclude from this that when Vb = 5.000 mL, we can calculate pH by using a weak base calculation for a solution of the weak base B with F′ = 0.2500 mmol / (25.00 + 5.00) mL, and that when Vb = ½Ve = 2.500 mL the chemical amounts of BH+ and B will be equal, and pH = pKa = 10.645.
Once the titration begins, the chemistry taking place is given by the equation
BH+ + OH− → B + H2O
which shows that each addition of OH− stoichiometrically converts BH+ to the conjugate weak base B. Since there is a mixture of the weak acid and its conjugate weal base, we say "Aha, a buffer!" and use the Henderson-Hasselbalch equation to calculate pH for all of the range 0 < Vb < Veq.
The pH calculation for Vb = Veq, discussed above, can be explicitly performed
[OH−] = √F′Kb = { (0.2500 mmol / 30.00 mL) · 1010.645−14.000 }½ = ( 0.00833333 · 4.4157 × 10−4 ) ½
[OH−] = 0.0019202 M
pH = 14.00 − (−log[OH−]) = 14.00 − 2.72 = 11.28
There is a bit more of a difference between approximate and exact (quadratic formula) calculations here, since the conjugate base B of the very weak acid BH+ is a relatively strong weak base. (Note that the value obtained for [OH−] is a significant percentage of F. This is a sign that our approximation is inaccurate. When x (corresponding to [H+] or [OH−] in weak acid or weak base calculations, respectively) is 5% or more of F, use of the the quadratic formula solution is advised. The pH obtained in this case by using the quadratic formula is 11.23.
Once we have reached equivalence, there is no more B to react with additional hydroxide, so for Vb > Veq, the continued addition of the titrant will only provide excess amounts of OH−, and we will use a strong base calculation, with [OH−] = F′ = mmol excess OH−/ total volume. For Vb = 10.00 mL = Veq + 5.00 mL,
[OH−] = ctitrant· (Vb − Veq ) / (Vb + Vanalyte ) = (0.0500 mmol/mL)(5.00 mL) / (10.00 mL + 25.00 mL)
[OH−] = 0.007143 M
pOH = 2.146
pH = 11.854
(The sketch of the titration curve is left as an exercise)
Problem 11-3. (ECA4, p.259) The base association constants of phosphate are Kb1 = 0.024, Kb2 = 1.58 × 10−7, Kb3 = 1.41 × 10−12. From the Kb values, calculate Ka1, Ka2, and Ka3 for H3PO4.
Solution: Using the relationships between the Ka and Kb values established for a triprotic system,
Ka1·Kb3 = Ka2·Kb2 = Ka3·Kb1 = Kw
we find the Ka values for phosphoric acid and its dissociated forms as
Ka1 (first acid dissociation constant):
H3PO4 ⇔ H+ + H2PO4− Ka1 = Kw/Kb3 = (1.00 × 10−14) / (1.41 × 10−12) = 7.09 × 10−3
Ka2 (second acid dissociation constant):
H2PO4− ⇔ H+ + HPO42− Ka2 = Kw/Kb2 = (1.00 × 10−14) / (1.58 × 10−7) = 6.33 × 10−8
Ka3 (third acid dissociation constant):
HPO42− ⇔ H+ + PO43− Ka3 = Kw/Kb1 = (1.00 × 10−14) / (0.022) = 4.2 × 10−13
Problem 11-25. (ECA4, p.261) A 100.0-mL aliquot of 0.100 M diprotic acid H2A (pKa1 = 4.00, pKa2 = 8.00) was titrated with 1.00 M NaOH. At what volumes are the two equivalence points? Find the pH at the following volumes of base added (Vb) and sketch a graph of pH versus Vb: 0, 5.0, 10.0, 15.0, 20.0, and 22.0 mL.
Solution: First, to calculate equivalence points, we determine just how much titratable H2A is present:
VH2A· cH2A = (100.0 mL)(0.100 M) = (100.0 mL)(0.100 mmol mL−1) = 10.0 mmol H2A
Thus, we'll need 10.0 mmol OH− to reach the first equivalence point (stoichiometric conversion of H2A to HA−) and an additional 10.0 mmol OH− to reach the second equivalence point (complete conversion of H2A to A2−), or 20.0 mmol total to reach the second equivalence point. Since the concentration of the NaOH titrant is 1.00 M, the calculation is simple: Each 1.00 mL of 1.00 M NaOH supplies 1.00 mmol OH−. So Ve1 = 10.0 mL and Ve2 = 20.0 mL.
Next, we can easily determine the pH at intermediate volumes and the first equivalence point by recognizing that 5.0 mL NaOH is ½Ve1, where the conversion of H2A to HA− has gone exactly halfway, so that [H2A] = [HA−]. Thus at Vb = 5.0 mL, pH = pKa1 = 4.00. Next, we recognize the titration mixture at Ve1 to be a solution of the intermediate species HA− of some formal concentration F′. However, we care little about the value of F′ here because the pH of a solution of an intermediate species like is nearly independent of concentration. The formula pH = ½(pKa1+ pKa2) here yields pH = 6.00 at Vb = Ve1 = 10.0 mL. A third easy pH value we can get is at Vb = 15.0 mL. Here the conversion of HA− to A2− has proceeded exactly halfway, so that [HA−] = [A2−]. Henderson-Hasselbalch tells us that here pH = 8.00. These theee pH values were obtained by very simple stoichiometric reasoning and trivial calculations - the only requirement is that we recognize the chemical situation and apply the appropriate means of determining the pH. Recognizing these "easy" cases will be invaluable to you as quick routes to solutions, especially on an exam!
The "tough" cases are the pH values at (i) Vb = 0, where we have a 0.100 M solution of the weak acid HA−, (ii) Vb = Ve2 = 20.0 mL, where we have a solution of the weak base A2− of some formal concentration F″, and (iii) Vb > Ve2 , that is beyond 20.0 mL where we calculate pH by treating the titration mixture as a strong base with a certain amount of excess OH−. Let's deal with the latter first. Since we have the equivalence volume(s), we can calculate excess as
excess OH− = (Vb− Ve2) cbase = (22.0 mL − 20.0 mL)(1.00 M) = (2.0 mL)(1.00 mmol mL−1) = 2.0 mmol
Next, sum the volumes Vb and the starting volume of the H2A analyte solution:
Vtotal = Vb + Va, initial = 22.0 mL + 100.0 mL = 122.0 mL
So we can obtain [OH−] as
[OH−] = 2.0 mmol / 122.0 mL = 1.639 × 10−2 M
The pH can now be obtained without much additional trouble:
[H+] = Kw / [OH−] = 1.00 × 10−14 / 1.639 × 10−2 = 6.10 × 10−13 M ⇒ pH = 12.21
Case (i) is an example of a weak acid calculation. We should always look to see if we can use the approximation
[H+] ≈ (FKa)½
which always works adequately as long as the value of Ka is no more than a few percent of F. That condition is certainly fulfilled here because F = 0.100 M, and Ka1 is only 1/1000th of that. Using this, we obtain
[H+] ≈ (FKa)½ = (0.100)(1.00 × 10−4)½ = 3.16 × 10−3 M ⇒ pH = 2.50
Finally, the most troublesome is the weak base calculation that we must perform at Vb = Ve2 . But even here we can make our job easier by applying the approximation
[OH−] ≈ (F′Kb1)½ = {(10.0 mmol A2−)(120.0 mL)−1 (1.00 × 10−6 )}½ = 2.88675 × 10−4 M
[H+] = Kw / [OH−] = 1.00 × 10−14 / 2.88675 × 10−6 = 3.464 × 10−11 M ⇒ pH = 10.46
Note that we used Kb1 = Kw / Ka2 and that F′ = 10/120 = 8.33 × 10−2 M, which is close to five orders of magnitude greater than Kb1, so our approximation is completely adequate.
In class we sketched the titration curve, and I'll reproduce one here later, time permitting. We also carried out a principal species analysis using this example - see the Lecture 11 webpage.
Example problem 1. Principal species analysis of a polypeptide. Consider the polypeptide (or "peptide", for short) with the amino acid sequence (amino to carboxy terminal) Lys-Pro-Gln-Asp-Arg-Thr. What is the net charge on the polypeptide at pH 7.4?
Solution: The amino acids of the peptide are lysine (Lys), proline (Pro), aspartate (Asp), arginine (Arg), and threonine (Thr). At a near-neutral pH, the amino and carboxyl termini of the peptide should carry one positive and one negative, respectively. Lys and Arg side chains would contribute one more positive charge each. The side chain of Asp will be negatively charged. The side chains of Pro, Gln, and Thr are neutral for practically all pH values within aqueous systems. Taken together we would predict a net charge of −1 at this pH.
Problem 8-24. (ECA5, p.187) Calculate the pH and fraction of dissociation of (a) 10−2.00 M and (b) 10−10.00 M barbituric acid. ( Ka = 9.8 × 10−5 )
Solution: This is a weak acid equilibrium calculation. We can write a table to help us define the equation we need to solve. We will adopt the convention used in the text denoting the initial concentration of the acid by F (or "formal" concentration).
| HA | = | H+ | + | A− | ||||
| initial concentration | F | 0* | 0 | |||||
| change in concentration | ||||||||
| final concentration | F − x | x* | x | |||||
The asterisk attached to the concentrations of H+ means that it is not, strictly speaking, zero initially, or derived solely from the dissociation of HA, but a small amount (~10−7 M) comes from the autodissociation of water. We will for the most part only deal with problems where this can be safely neglected, but we should keep in mind the need to verify that this assumption is valid.
The next step in this problem is to substitute the quantities in the final concentration row into the expression for Ka and solve the resulting equation for x, plugging in numbers for F and Ka.
Ka = [H+][A− ] / [HA] = x2 / F − x
Solving the above for x yields a quadratic equation:
x2 + Kax − KaF = 0
We have kept the equation in general form, and we can write the general form of the solution for this type of problem using the quadratic formula. The solution ("roots") to the equation
ax2 + bx + c = 0
has the formula
x = { −b ± ( b2 − 4ac)1/2} / 2a .
Thus, with a = 1, b = Ka, and c = −KaF, we can write the general formula for the solution as
x = { −Ka ± (Ka2 + 4KaF)1/2} / 2 .
Plugging in the numbers Ka = 9.8 × 10−5 and F = 10−2.00 = 0.010, and discarding the negative root, we obtain
x = 9.4216 × 10−4,
from which we obtain [H+] = 9.4 × 10−4 and pH = 3.03.
The fraction of dissociation, α, can be directly computed as x / F.
α = 9.4216 × 10−4 / 10−2.00 = 9.4216 × 10−2 = 0.094 or 9.4%
For the case where F = 10−10.00 , we do not obtain the pH from solving a quadratic equation derived from the HA equilibrium. Rather, the pH is set to that of pure water, because H+(aq) from the acid HA at this concentration is insignificant in relation to the H+(aq) from autodissociation of water. So, the pH is 7, and the fraction of dissociation is found by
[A− ] / ( [HA] + [A− ] ) = Ka / ( Ka + [H+] ) = 9.8 × 10−5 / ( 9.8 × 10−5 + 1.0 × 10−7) = 0.99898
The acid is 99.9% dissociated at this concentration!
Example Problem: Weak acid pH calculation
For a weak acid HA, with pKa = 2.328, calculate the pH of a 0.0500 M solution.
Solution: This is a weak acid calculation. In this case, we start with a weak acid, made into a(n aqueous) solution of a given concentration, and calculate the pH using the acid dissociation equation and its associated Ka value. Why does the acid dissociation equation govern the pH? It is because we start with only HA, and the pH will change according to the extent of dissociation of HA:
HA = H+ + A− Ka = [H+][A− ] / [HA].
Note that the Henderson-Hasselbalch equation does not apply here because we are not starting with a mixture of HA and A−. If we were to start with only A−, then we would be dealing with a weak base calculation, and the relevant chemical equation would be the base hydrolysis reaction, with equilibrium constant Kb.
One thing that we need to do to solve this problem - and we may as well do it first off - is to derive Ka from pKa.
pKa = − log10Ka iff Ka = 10−pKa
Thus,
Ka = 10−2.328 = 4.70 × 10−3
where we have followed the rule for treating significant figures when we take the antilog of a number.
We can write a table to help us define the equation we need to solve. Using the convention denoting the initial concentration of the acid by F (or "formal" concentration), and letting x be the quantity we need to solve for, we have:
| HA | = | H+ | + | A− | |||
| initial concentration | F | (10−7 M) | 0 | ||||
| change | − x | + x | + x | ||||
| final concentration | F − x | + x | + x | ||||
(Note: In all such problems
we will need to solve in this context, we will be able to safely
ignore the small amount
(10−7 M) of H+
coming from the autodissociation of water, relative to that coming
from the dissociation of HA. But it is important to understand
that there are situations when this assumption breaks down.)