GENERAL CHEMISTRY TOPICS
Electromagnetic radiation and quantum theory
The quantum nature of EM radiation and its interaction with matter
The quantum nature of EM radiation and its interaction with matter
Although classical physics had explained most of its behavior as a result of its wave nature, Planck and Einstein showed that electromagnetic (EM) radiation behaves as if its energy is carried at the nanoscale in small bundles, or quanta (plural of quantum), of energy with particle-like characteristics. The behavior of EM radiation in its interactions with matter is, in fact, where this quantum nature is most clearly revealed.
We know that the light of the sun can provide a pleasant warmth, but overexposure of the skin to sunlight results in a burn. This burning, which suggests a light-induced chemical change, is due to the UV component of the sun's radiation. Our experience with sunlight conforms to the idea that EM radiation can deliver its energy to matter as it is absorbed. How this absorption occurs at the atomic and molecular scale cannot be accounted for by the wave model.
Black body radiation
As anyone who has observed the glow of a hot iron will attest, matter emits EM radiation as a result of its thermal energy. When this is given off under idealized conditions it is called black body radiation. The emission spectra of black body radiation at different temperatures (see illustration below), which defied prediction by classical physics, could be explained if, for each frequency (recall that frequency is inversely proportional to wavelength), the possible energies of the oscillators (oscillating charges within matter give rise to black body EM radiation) were restricted to values proportional to integral multiples of the oscillator frequency, that is, E = nhν, where E is the energy of the oscillator and ν is its frequency, n is a positive integer (n = 1,2,3,...) , and h is a proportionality constant. This implied the oscillators carried energy in discrete “packets” or quanta. This insight was due to German physicist Max Planck, who advanced his hypothesis in 1901. Planck chose the value of the proportionality constant h - which became known as Planck's constant (h = 6.6260688 × 10–34 J·s) - to fit the experimentally observed spectra of emission from glowing objects.
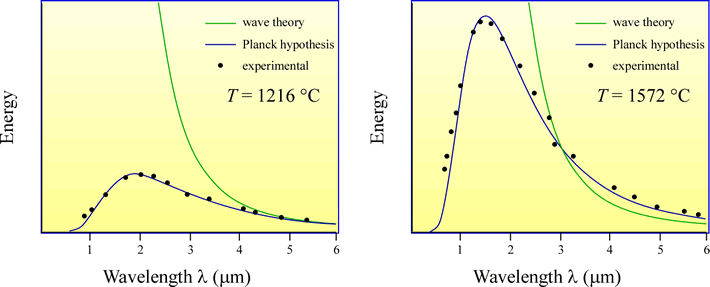
Above: Illustration of the observed black body radiation spectrum for two different temperatures. The dots indicate experimental measurements of the amount of energy, or intensity of radiation, emitted at a given wavelength, whereas the predictions from wave theory are shown by the green curves. Wave theory made reasonably good predictions for long wavelengths, but utterly failed for short wavelengths, for which the theory predicted that energies should tend toward infinity as the wavelength approached zero. This clearly untenable prediction was known as the "ultraviolet catastrophe". Note that the visible range of EM radiation is at the far left of each graph, from 0.4 to 0.7 µm. Planck's hypothesis led to a satisfactory prediction of blackbody radiation intensities for all wavelengths.
Photoelectric effect
For certain materials, especially metals, an electric current can readily be measured upon illumination of its surface, under vacuum, with light of sufficiently short wavelength. What occurs here is that light provides the energy to ionize the material. The chemical equation representing this process is
A + light → A+ + e−
where A is the material undergoing photoionization. This helps clarify why the photoelectric effect was first observed for metals, as they have the lowest ionization energies, although, in principle it can be observed in any material as long as sufficiently short EM wavelengths are employed. The electrons produced and measured as current are essentially the same phenomena as Thomson's cathode rays, but the excess kinetic energy of the ejected electrons, or photoelectrons, showed an interesting dependence on the wavelength of the illuminating light. First of all, no photoelectrons are observed until the frequency of light reaches a minimum, threshold value. Let us denote this threshold frequency as ν0. Thereafter, as frequency, ν, is increased (and wavelength, λ, decreases), the kinetic energy of the photoelectron increases linearly with the frequency. Since energy is conserved, the energy from the incident light must be equal to the sum of the ionization energy of A plus the kinetic energy of the photoelectron
light energy = IEA + KE
Note that in some accounts of the photoelectric effect (e.g. Ref. 2), the ionization energy, or binding energy of the electron to the atom, is represented as W (corresponding to the historical term "work function" from solid-state physics). Significantly, the ability of light to generate at least some of this photocurrent did not depend on its intensity - as predicted according to the wave model. Albert Einstein provided a theoretical explanation for the photoelectric effect in 1905 by making use of Planck's quantum hypothesis, and suggesting the name photon for quanta of light. Einstein proposed that each such photon carried an energy E according to the relation (often called the Planck-Einstein relation):
E = hν
The factor h is Planck's constant introduced above, and combining this with the equation relating frequency, wavelength, and wave speed leads to
E = hc / λ
an alternate form of the relation, useful for converting between EM wavelength and energy.
In the figure below, the EM spectrum is re-presented, here with energies (expressed as kJ/mol) given in a scale along with the wavelengths and frequencies.
Above: Diagram of EM spectrum showing correspondence between energies and atomic and molecular transitions
Thus, EM radiation displays a dual nature - in many respects it behaves like a wave, yet in other respects it shows a particle-like nature. One key feature of photons that emerges from Einstein's theory is that photons have a rest mass of zero, yet since they travel at the speed of light, they carry momentum, just like a particle.
Absorption and emission: The interaction between matter and light
We are now in a position to appreciate the basis for the interactions between light and matter- in particular the processes of absorption and emission. The quantum nature of both light (EM radiation) and the atom govern these phenomena.
Excitation and emission spectra. When atoms are subjected to the input of a large amount of energy, many of them are promoted to a higher energy state. They subsequently emit light of only certain characteristic wavelengths, with the atom returning to its lower energy state. The process of putting energy into a collection of atoms is called excitation, while the pattern of characteristic wavelengths emitted by the atoms in response to excitation is called the emission spectrum of that atom type.
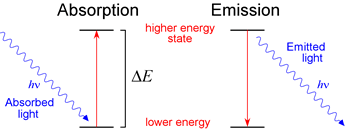
Absorption and emission. An atom in a lower energy state can absorb light of frequency ν and thereby be promoted to a higher energy state, provided hν = ΔE, where ΔE is the difference in energy between the two states of the atom. Emission is the reverse of this process.
Absorption. The input of energy in the form of EM radiation drives the absorption by atoms of certain characteristic wavelengths of the EM spectrum. It is absorption by substances of some visible wavelengths, and transmission or reflection of others, that results in what we perceive as the colors of those substances. Absorption is in essence an excitation, and absorption by an atom is commonly followed by emission of a wavelength of equal to or longer than the wavelength absorbed.
The specialized pigment molecules of photosynthesis - principally chlorophyll - are highly conjugated molecules with absorption frequencies in the visible range. The Planck relationship states that the energy of a photon of electromagnetic radiation is proportional to its frequency, and inversely proportional to its wavelength. When this energy corresponds to the difference between energies of electronic molecular orbitals, the photon may be absorbed and its energy then appears as an excited state of the molecule - that is, an electron is promoted to a higher energy molecular orbital.
But this excited state is short-lived. Four potential fates of the excited state concern us here.
(1) Internal conversion - the energy is dissipated into molecular rotational and vibrational modes. This is basically entropic loss.
(2) Fluorescence - the molecule may emit a photon, typically a longer wavelength than the absorbed photon.
(3) Photooxidation - the molecule in its excited state holds on to that electron a little less tightly, making this species - if it has a long enough lifetime - a better reducing agent. If the electron in the higher energy state is transferred to an acceptor species and away from the original excited molecule, that latter molecule has been oxidized.
(4) Exciton transfer (also called resonance energy transfer) - the energy of the excited state can be transferred to a nearby molecule. This is also an important process in photosynthesis, as there are many more pigment molecules than the number that actually undergo photooxidation.
Together, proceses (3) and (4) are the essence of the efficient harvesting of light energy in photosynthesis.
Important units
Planck constant: h = 6.62606931 × 10−34 J·s (ref 1)
Speed of light, c = 2.99792458 × 108 m·s−1
Elementary charge, e = 1.60218 × 10−19 C