GENERAL CHEMISTRY TOPICS
Acid-base equilibria
Weak acids and bases. The acid dissociation equation and the general weak acid equilibrium. The base hydrolysis equation and the general weak base equilibrium.
The acid dissociation equation and Ka
The acid dissociation equation for a general acid HA
HA = H+ + A−
is defining for the acid dissociation constant, Ka:
Ka = [H+][A– ] / [HA]
Ka provides a quantitative measure of acid strength. For strong acids, Ka is very large. Hydrochloric acid, for example, has a Ka ≈ 106, which means HCl(aq) is virtually completely dissociated. This is typical for strong acids, and they are classified (as are soluble ionic compounds) strong electrolytes. For a weak acid such as acetic acid, HC2H3O2, Ka is approximately 1.8 × 10−5, a value which indicates acetic acid in water remains mostly unionized. This is shown by a conductivity test with a 5% acetic acid solution, which shows the solution can conduct some, but very much less current than a solution of sodium chloride at a similar concentration. The acid dissociation equation for acetic acid is shown at right.
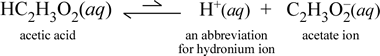
By representing hydronium as H+(aq), the ionic equation for acetic acid in water is formally balanced without including a water molecule as a reactant, which is implicit in the above equation.
The general weak acid equilibrium: a quantitative treatment
For a weak acid equilibrium calculation, an "ICE" table is extremely useful. Such a table helps define the equation needed to solve the general problem. We will adopt the convention of denoting the initial concentration of the acid by F (or "formal" concentration).
| HA | = | H+ | + | A− | ||||
| initial concentration | F | 0* | 0 | |||||
| change in concentration | ||||||||
| final concentration | F − x | x* | x | |||||
The asterisk attached to the concentrations of H+ means that it is not, strictly speaking, zero initially, or derived solely from the dissociation of HA, but a small amount (~10−7 M) comes from the autodissociation of water. We will for the most part only deal with problems where this can be safely neglected, but we should keep in mind the need to verify that this assumption is valid.
The next step in this problem is to substitute the quantities in the final concentration row into the expression for Ka and solve the resulting equation for x, plugging in numbers for F and Ka.
Ka = [H+][A− ] / [HA] = x2 / F − x
Solving the above for x yields a quadratic equation:
x2 + Kax − KaF = 0
We have kept the equation in general form, and we can write the general form of the solution for this type of problem using the quadratic formula. The solution ("roots") to the equation
ax2 + bx + c = 0
has the formula
x = { −b ± ( b2 − 4ac)1/2} / 2a .
Thus, with a = 1, b = Ka, and c = −KaF, we can write the general formula for the solution as
x = { −Ka ± (Ka2 + 4KaF)1/2} / 2 .
The pH calculation for a weak acid
The solution to this problem is generally obtained as the positive root of a quadratic equation, denoted as x above, determined by the values of the parameters F (formal concentration) and Ka. The value of x is then assigned to equilibrium concentrations [H+] and [A−] for the case of the dissociation of a weak acid HA.
Example problem. For acetic acid, with Ka = 1.8 × 10−5, calculate the pH of a 0.10 M solution.
Solution: This is a weak acid calculation. Using the given values of F (0.10) and Ka, the formula for the positive root of the quadratic equation above yields x = 1.3327 × 10−3. Setting x = [H+] and calculating −log x, the pH (reported to the hundredths place) is 2.88.
However, we often make use of an approximation of this solution:
x ≈ (FKa)1/2
How does this arise and under what circumstances is it acceptable to use in place of the exact quadratic equation solution? The validity of this method hinges on whether x can be neglected compared to F. If so, then we can write
Ka = x2 / (F – x ) ≈ x2 / F
where we read "≈" to mean "about (approximately) equal to". Rearranging as x2 ≈ FKa and taking the square root of both sides yields the approximation given above.
The table below compares the exact versus approximate solutions for several instructive cases.
Weak acid pH calculations: Exact vs approximate solution |
||||||
formal |
Ka | fraction |
pHexact | pHapprox | ||
|
0.1 M |
10−4 |
0.0311 |
2.507 |
2.500 |
||
0.1 M |
10−5 |
0.00995 (≈ 0.01) |
3.002 |
3.000 |
||
0.1 M |
2.63 × 10−4 |
0.05 |
2.301 |
2.290 |
||
|
0.01 M |
10−6 |
0.00995 (≈ 0.01) |
4.002 |
4.000 |
||
The judgment of whether the approximate value for pH is an adequate substitute for the exact value depends on the context. If one can automatically solve the quadratic equation (using an Excel spreadsheet or programmed calculator), then of course the exact solution would be routinely used since it can be obtained with minimal effort. But if we are forced to calculate pH by hand, it is a considerable savings in labor to use the approximate formula. We can assess the error introduced and decide what fractional or absolute difference between pHapprox and pHexact we are willing to tolerate. Bear in mind as well that even an exact calculated pH may well differ from what we might actually measure experimentally for a variety of reasons (that we'll have to set aside as an advanced topic). In our text (Ref 1) if the value α = x/F < 0.05, the approximation is deemed adequate. Row 3 in the table above shows that for α = 0.05, the error in pH is still only on the order of 0.01 pH unit. In this particular case, (KF)1/2 = {(0.10)(1.8 × 10−5)}1/2 = 1.342 × 10−3, and pH = 2.87.
The base hydrolysis equation and the definition of Kb
Kb is known as the base hydrolysis constant, or simply "base constant". It is defined by the chemical equation for abstraction by a base of a proton from water, called the base hydrolysis equation.

Note that the base hydrolysis equation is a complete Brønsted-Lowry acid-base reaction, with water as the reactant acid. The expression for the base constant is derived by following the usual rules for writing an equilibrium constant for a chemical reaction, with the additional feature that the concentration of water is dropped from the expression. This is because in dilute aqueous solution, the concentration of water remains practically constant.
The simple molecular compound ammonia (NH3) acts as a neutral weak base according to its base hydrolysis equation,
shown as a reactant-favored equilibrium. The expression for Kb for ammonia is given as [NH4+][OH−] / [NH3] and an experimental value for it is approximately 1.8 × 10−5.
Example problem. For ammonia, with Kb = 1.8 × 10−5, calculate the pH of a 0.050 M solution.
Solution: This is a weak base calculation and we'll use the formula for the approximate solution for the positive root of the quadratic equation that results from the ICE table entries for equilibrium concentrations substituted into the expression for Kb. Note that these expressions take the same form as those for the case of the weak acid dissociation equilibrium, with x = [OH−] and Kb taking the place of Ka. Using the given values of F (0.050) and Kb, (KF)1/2 = {(0.050)(1.8 × 10−5)}1/2 = 9.487 × 10−4, and pOH = 3.02. Using the formula pH = 14.00 − pOH, the pH (reported to the hundredths place) is 10.98 (the exact solution in this case yields pH = 10.97).
[OH−] = x ≈ (FKb)1/2 pH = 14.00 − pOH ≈ 14.00 + log x