GENERAL CHEMISTRY TOPICS

Chemical kinetics: Rate laws

Rate laws and rate constants. Reaction order: Overall reaction order and individual reaction order. Determination of rate law equations using experimental measurements of intial rates.

---

Rate laws, rate constants, and reaction order

Given that we have carefully thought about what is meant by reaction rate, we can investigate quantitative relationships between the rates and chemical concentrations. Experimental measurements of a great many reactions carried out at constant temperature show regularities in concentration dependence of rate that take the form of simple mathematical relations. These equations are called the rate laws.

Consider a simple chemical reaction with only one reactant. Let c be the concentration of this reactant (for example, c = [N₂O₅] in the figure below), let n be its stoichiometric coefficient, and let t represent the time variable. As we have seen, measuring c as the reaction progresses, and graphing as a function of time, yields a progress curve. To review, the average rate, over a time interval Δt, is given by −Δc/Δt. In making this time interval very small, the average rate approaches the instantaneous rate V, at any time point within the interval. The instantaneous rate at any time t is the slope of the tangent to the curve at that value for t. The instantaneous rate when the reaction starts at time t = 0 is the slope of the tangent to the progress curve for t = 0 and is called the initial rate. We'll often use V₀ to symbolize the initial rate.

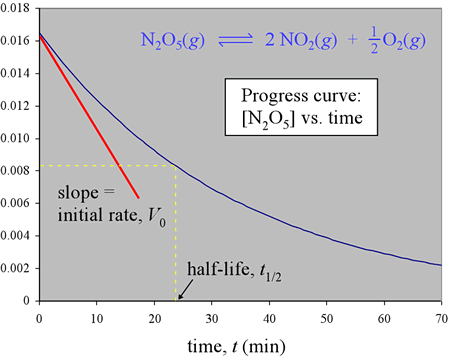
When progress curves for a reaction are determined experimentally, they reveal patterns in the dependence of rate on concentration. By consistently determining the initial rate of a reaction as initial concentration is varied, it is found that initial rates depend on starting concentrations as expressed by the equation

V₀ = kc^m

where V₀ represents the initial rate, and the constant k and exponent m are chosen to fit the experimental data. This equation is called the rate law. The constant k is called the rate constant. We call m the order of reaction, and most common are m = 1 and 2. If m = 1, the reaction is first-order in c, and if m = 2, it is second-order in c.

We can also look at the half-life (t_1/2) of a reaction. The half-life is the time required for one-half of the initial reactant to be consumed. Once the rate law for a reaction is determined, the reaction half-life can be calculated from it.

Reaction order: overall and individual

Let's generalize the above to deal with the case where there are an arbitrary number of reactants. When the initial rates for the reaction

aA + bB + cC + ····   =   xX + yY + zZ + ····

are measured at a fixed temperature, the rate law can be expressed in general by the equation

V₀ = k[A]^m[B]ⁿ[C]^p ····

for some rate constant k and numbers m, n, p,... that are usually, but not always, non-negative integers. The rate constant is a characteristic of a particular reaction and reaction mechanism and varies with temperature. This is a fact worth remembering, especially in experimental work. The reaction progress data used to elucidate the rate law must be carried out under constant temperature conditions.

A distinction we make when the rate law contains concentration terms for more than one chemical species concerns reaction order. The overall order is given by the sum m + n + p + ···· , while each individual reactant is assigned an individual order: the reaction is of order m in reactant A, order n in reactant B, order p in reactant C, etc. Note that the numbers m, n, p,... in a rate law are not necessarily related to the stoichiometric coefficients of A, B, C,..., respectively, in the balanced chemical equation for the reaction. The sum of the individual orders equals the overall order. We often associate the reaction order with the rate constant by referring to a zero-order rate constant, first-order rate constant or second-order rate constant, etc. Note how the units of the rate constant k will depend on the overall order of the reaction.

Example problem: Reading the overall and individual orders from the rate law, and deriving the units for the rate constant. For the reaction

BrO₃⁻(aq)  +  5 Br⁻(aq)  +  6 H⁺(aq)  =  3 Br₂(aq)  +  3 H₂O(aq)

the following rate law was determined:

V₀  =  k [BrO₃⁻] [Br⁻] [H⁺]²

(a) What is the (overall) order for this reaction and what are the individual orders?
(b) What are the units for the rate constant k in this case?

Solution. (a) The overall order is four, since the [BrO₃⁻] and [Br⁻] terms have exponent of one, and the [H⁺] term has an exponent of two. These individual orders (first order in BrO₃⁻, first order in Br⁻, second order in H⁺) sum up to the overall order. (b) The strategy to employ here is dimensional analysis, bearing in mind that reaction rate can always be expressed in the units M s⁻¹ (equivalent to mol L⁻¹s⁻¹).

M s⁻¹ = (units of k)(M)(M)(M²) = (units of k)((M⁴)

units of k = (M s⁻¹) / (M⁴) = M⁻³ s⁻¹

In general the units for the rate constant k will be M ^{(1−overall order)}·s⁻¹. In some cases, reaction rates may be expressed using minutes or some other time denomination as the time unit, and decimal multiples of molarity may be used (e.g. the units µM min⁻¹ are possible for reaction rate).

A very important type of problem we need to solve is how to use experimental kinetics data to deduce the form of the rate law. For two or more participating reactants, a systematic series of experiments is carried out in which the starting concentration of one reactant is varied, while the other(s) are held constant, and the initial rate is measured (by analysis of the progress curve). By comparing these results, we can determine the individual order for the reactant being varied. Other trials are performed, as required, individually varying the other reactant(s), to determine the other individual order(s). The following example problem takes us through this process.

Example problem: Determining the rate "law and order" from experimental data⁴: In a study of the reaction of pyridine (C₅H₅N) with methyl iodide (CH₃I) in a benzene solution, the following reaction rates were measured at 25 °C for different initial concentrations of the two reactants:

		[C5H5N]
				[CH3I]		Initial Rate
		(mol L−1)		(mol L−1)		(mol L−1s−1)
		1.00 × 10−4		1.00 × 10−4		7.5 × 10−7
		2.00 × 10−4		2.00 × 10−4		3.0 × 10−6
		2.00 × 10−4		4.00 × 10−4		6.0 × 10−6
	(a) Write the rate law for this reaction. (b) Calculate the rate constant (k) for this reaction. (c) Predict the initial reaction rate that would be seen in a solution in which [C5H5N] is 5.0 × 10−5 M and [CH3I] is 2.0 × 10−5 M.