BIOCHEMISTRY TOPICS
Michaelis-Menten equation
Assumptions underlying the mechanistic model that leads to the Michaelis-Menten equation.
Given that enzyme-catalyzed reactions display hyperbolic initial rate vs. substrate concentration curves, what can be said generally about the underlying reaction mechanism? What type of mechanistic model - meaning the sequence of elementary reactions involving substrate, enzyme, any intermediates or accessory molecules that sum up to the substrate to product reaction - accounts for hyperbolic kinetics?
Consider the simple model for the enzymatic catalysis of the reaction converting a substrate S to a product P, consisting of three elementary reactions, or mechanistic steps, shown below. We will derive an expression for the initial rate of the enzyme catalyzed reaction represented by this model, which we will call the Michaelis-Menten equation.
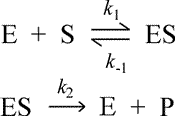
Three rate constants are defined in this model: the forward rate constant k1 for the bimolecular formation of the enzyme-substrate (ES) complex from free enzyme and unbound substrate; the reverse rate constant k−1 for the unimolecular dissociation of ES back to E + S; and the rate constant for the catalytic step, k2, i.e. the rate constant for the unimolecular breakdown of ES to E + P. For the moment, no assumption is made about a rate limiting step.
Since the forward reaction velocity is equal to the rate of appearance of product, initial rate V0 is fundamentally dependent on the concentration of ES, and is given by the equation V0 = k2[ES]. As an intermediate in the mechanism, the concentration of ES is not directly under experimental control, and may be difficult or practically impossible to measure.
There are two alternative assumptions that can be made to obtain an expression to substitute for [ES]. The first is to simply assume (as was done in the discussion of enzyme kinetics) that ES is in equilibrium with E + S, which is effectively equivalent to assuming the second forward step is rate determining. Note that in the absence of a catalytic step, ES and E + S would reach an equilibrium, with an equilibrium constant Keq = k1/k−1. We define a dissociation constant, Kd, which is the inverse of Keq. Binding affinities are often measured or reported in terms of Kd. A lower Kd means a tighter complex; a higher Kd means a weaker complex.
The alternative to the equilibrium assumption, namely the steady-state assumption, is more generally applicable to enzyme-catalyzed reactions. It is based upon observations in cases for which it it is possible to measure the concentration of the enzyme-substrate concentration over time. These observations reveal that after an extremely short burst phase required for ES to build up, its concentration remains constant. In other words, the rate at which ES forms is exactly balanced by the rate at which it is removal. If this condition is applied to the elementary steps of the mechanistic model presently under consideration, the following relation is obtained.
k1[E][S] = k−1[ES] + k2[ES] = (k−1 + k2)[ES]
It is worth emphasizing that this equation, which provides a starting point for derivation the Michaelis-Menten equation, is the result of application of the steady state assumption to the mechanism specified. By mechanism, we mean the set of elementary reactions, the sum (or net result) of these reactions is the stoichiometrically correct chemical equation for conversion of substrates to products, and which is consistent with the observations of reaction velocity under varying conditions - particularly the dependence of initial reaction velocity upon concentration of substrate. In other words, the mechanistic model will predict the initial reaction rate's dependence on substrate concentration, which is expressed by the Michaelis-Menten equation.
To continue with the derivation of the rate equation for our simple kinetic model, we note the relation between the concentrations of free enzyme, the enzyme-substrate complex, and the total enzyme. In the case where substrate is present in significant excess over enzyme - a reasonable condition since enzymes accelerate reactions in amounts substoichiometric to substrate - the analysis is simplified. We can then solve explicitly for [ES] in terms of experimental "knowns" - the total enzyme and total substrate concentrations - and a parameter defined as KM that is a simple expression combining rate constants included in the model.
The total enzyme concentration, [E]T, is the sum of the concentrations of free enzyme E and the enzyme-substrate complex, ES (since free enzyme and enzyme-substrate complex are the only forms of enzyme included in the model):
[E]T = [E] + [ES]
Note that when substrate concentration is very large, most enzyme molecules will at any point in time have bound substrate, and there will be very little free enzyme:
[ES] ≈ [E]T ([S] very high)
A similar approximation holds for very low substrate concentration relative to enzyme, [E] ≈ [E]T ([S] very low), but for our present purposes, the expression
[E] = [E]T − [ES]
is used to substitute for [E] in the expression derived above from the steady state assumption:
k1([E]T − [ES])[S] = (k−1 + k2)[ES]
Dividing both sides by k1 and then collecting terms in [ES] on the right side,
[E]T[S] = {(k−1 + k2)/k1}[ES] + [ES][S]
and defining the parameter KM as (k−1 + k2)/k1, and rewriting the last expression as
[E]T[S] = KM[ES] + [ES][S] = (KM + [S])·[ES]
which now permits an expression for [ES] to be written:
[ES] = [E]T[S] / ([S] + KM)
Invoking the relation V0 = k2[ES] yields an equation for initial reaction velocity as a function of total enzyme concentration, substrate concentration, the parameter KM, and the catalytic step rate constant, k2. Labeling the latter as kcat,
V0 = kcat[ES] = kcat[E]T[S] / ([S] + KM)
One final definition to be made: As noted above, when substrate concentration increases to very high levels, it saturates the available substrate binding sites provided by enzyme, and [ES] ≈ [E]T. This translates to V0 ≈ kcat[E]T. The latter represents a theoretical maximum velocity (Vmax), which is approached in the limit of saturating amounts of substrate. Hence, the definition Vmax = kcat[E]T can be substituted in the last equation to yield what is commonly referred to as the Michaelis-Menten equation:
V0 = Vmax[S] / ([S] + KM)
An important point: Although this equation was derived using a particular simple mechanism, it is valid for many more complex mechanisms. It reproduces the saturation kinetics characteristic of enzyme-catalyzed reactions.
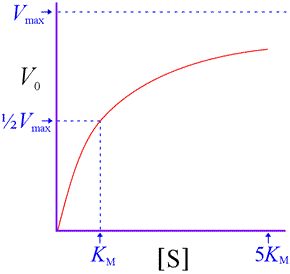
That is, V0 approaches a limit of Vmax as substrate concentration increases. We also see that KM represents a substrate concentration at which V0 reaches one-half Vmax. (Substitution of ½Vmax for V0 in the above equation and solving for [S] shows that [S] = KM. ) Note that [S] must be quite large before V0 becomes close to Vmax . For instance, at [S] = 5KM, the initial rate is only 83% of Vmax.
Related topics pages: