BIOCHEMISTRY TOPICS
Michaelis-Menten equation
Assmptions underlying the mechanistic model that leads to the Michaelis-Menten equation.
Consider the simple model for the enzymatic catalysis of a unimolecular reaction converting a substrate S to a product P, shown below. We will derive an expression for the initial rate of the enzyme catalyzed reaction represented by this model, which we will call the Michaelis-Menten equation.

Three rate constants are defined in this model: the forward rate constant k1 for the formation of the enzyme-substrate (ES) complex from free enzyme and unbound substrate; the reverse rate constant k−1 for the dissociation of ES back to E + S; and the rate constant for the catalytic step, k2, i.e. the unimolecular rate constant for the breakdown of ES to E + P. Note that in the absence of a catalytic step, ES and E + S would reach an equilibrium, with an equilibrium constant Keq = k1/k−1. We define a dissociation constant, Kd, which is the inverse of Keq. Binding affinities are often measured or reported in terms of Kd. A lower Kd means a tighter complex; a higher Kd means a weaker complex. The initial rate V0 of the forward reaction is fundamentally dependent on the concentration of ES, and is given by the equation V0 = k2[ES]. We can make two alternative assumptions to obtain an expression to substitute for [ES].
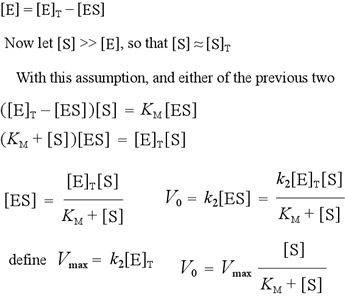
To continue with the derivation of the rate equation for our simple kinetic model, we note the relation between the concentrations of free enzyme, the enzyme-substrate complex, and the total enzyme. In the case where substrate is present in significant excess over enzyme - a reasonable condition since enzymes accelerate reactions in amounts substoichiometric to substrate - the analysis is simplified. We can then solve explicitly for [ES] in terms of experimental "knowns" - the total enzyme and total substrate concentrations - and the parameter KM. Then we use the expression V0 = kcat[ES] to express the measurable initial reaction rate in these terms, plus the additional parameter Vmax.
An important point: Although this equation was derived using a particular simple mechanism, it is valid for many more complex mechanisms. It reproduces the saturation kinetics characteristic of enzyme-catalyzed reactions.

That is, V0 approaches a limit of Vmax as substrate concentration increases. We also see that KM represents a substrate concentration at which V0 reaches one-half Vmax. (Substitution of ½Vmax for V0 in the above equation and solving for [S] shows that [S] = KM. ) Note that [S] must be quite large before V0 becomes close to Vmax . For instance, at [S] = 5KM, the initial rate is only 83% of Vmax.