GENERAL CHEMISTRY TOPICS
Chemical bonding
Chemical bonds: when atoms transfer or share valence electrons. Ionic bonds and covalent bonds. Ions and ionic compounds. The example of sodium chloride (an ionic compound) and lattice energy. Covalent bonds. The formation of diatomic hydrogen - the H2 molecule - as an illustration of the covalent bond and bond energy. Covalent compounds and molecules. Ionic vs. covalent bonds.
Overview of chemical bonding
We are concerned mainly with two types of bonding, ionic and covalent. The two types of bonding form the basis of the classification of compounds as ionic or molecular. Sodium chloride (NaCl) is a familiar example of an ionic compound, while water serves as a familiar example of a molecular compound. Ionic bonding arises from the attraction of oppositely charged species, a cation and an anion. Shared electrons form the "glue" that hold nuclei together in covalent bonds .
Water is an excellent example illustrative of many aspects of chemistry. The discussion that opens Chapter 4 in our text [Ref 1, §4.1] makes use of water by highlighting the physical and chemical difference between the elemental forms of the constituents of water - hydrogen H2(g) and oxygen O2(g) - and water itself.
Ions and ionic compounds
Since atoms can lose electrons to become cations or gain electrons to become anions, it is easy to imagine a reaction in which the atoms of an element give up one or more electrons to the atoms of a different element. In terms of reaction types, this can be classified as an oxidation-reduction (or "redox") reaction. For example,
4 Na(s) + O2(g) → { 4 Na+(g) + 2 O2−(g) } → 2 Na2O(s)
In this chemical equation, a representation of a chemical reaction, the net reaction is the conversion of the species on the left - the reactants, to the products - the species on the right. The bracketed species in the middle represent reaction intermediates that would result from a transfer of four electrons from each of four sodium atoms to an oxygen molecule with its concomitant fragmentation into two oxide anions. These two oppositely charged ions would attract one another due to the electrostatic force, and in fact form a crystalline solid in which the ions pack together, occupying alternate positions in a three dimensional lattice. Such ionic compounds form - as described above - between metals (which relatively easily give up electrons) and nonmetals (which relatively avidly accept extra electrons).
Sodium chloride (NaCl) is without question the most familiar example of an ionic compound. Ionic compounds form crystalline solids, made up of large domains of a regularly repeating three-dimensional arrangement of the component ions. This regular pattern, called the lattice, forms a network of Na+Cl− ionic bonds.
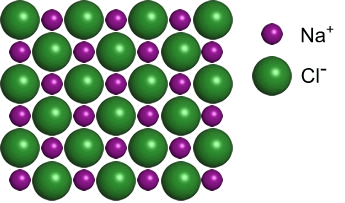
At right, a two-dimensional slice of the NaCl crystalline lattice is shown. The radius of the Cl− anion is 80% larger than the Na+ cation. This is not surprising since Na+ represents a filled first and second shell, while Cl− is three completed shells.
Let us consider for a moment the energy change associated with the chemical process of conversion of the elements sodium and chlorine to an ionic-bonded compound.
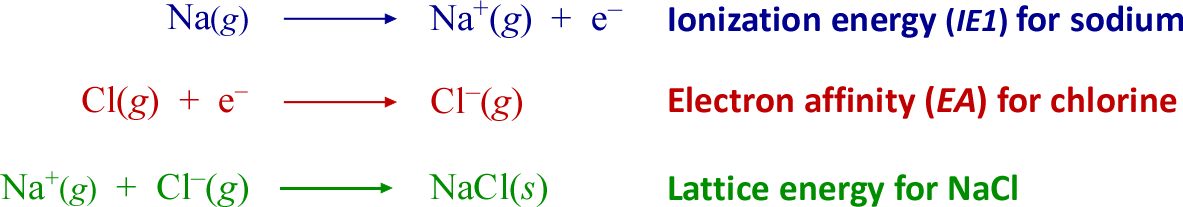
The change in energy for each of these three processes contributes to the overall energy change when sodium chloride forms from its elements. The first chemical equation represents the ionization of sodium in its gaseous form. This is termed the first ionization energy (IE1), which is always an energy-requiring, or endothermic process. For sodium, IE1 = 496 kJ/mol. The positive sign of the energy change is the convention for endothermic processes. The second process, the electron affinity (EA) of gaseous chlorine, is an exothermic process (by definition an energy-releasing process; the sign of the energy change in this case negative). The change in energy accompanying the acquisition of an electron by a neutral chlorine atom to form a chloride anion in the gaseous state is −349 kJ/mol.
Note that the sum of these first two processes would yield an energy change of (+496) + (−396) = +147 kJ/mol - if we can correspondingly sum the associated energy changes. This is indeed the case, and the result indicates that a transfer of the 3s electron from sodium (yielding the stable neon electron configuration for Na+) to chlorine, completing the latter's 3p subshell and yielding the same electron configuration as argon, still is an endothermic process. Nonetheless, the third step, which corresponds to what is termed lattice energy more than makes up for the energy required to form the ions from the neutral gas-phase atom and illustrates the strength of ionic bonds. The exothermic lattice energy for sodium chloride is −788 kJ/mol, an overwhelmingly favorable energetic contribution to the formation of this ionic compound from its elements. In general for binary ionic compounds, lattice energy makes the predominant exothermic contribution, providing the driving force favoring their formation from a metallic element plus a nonmetallic element.
It should be pointed out that ionic compounds are not limited to combinations of monatomic ions. They can also involve polyatomic ions. Examples are sodium nitrate, calcium acetate, and ammonium sulfate.
Covalent bonds
Covalent bonds form between atoms of nonmetals, such as hydrogen and oxygen, giving rise to molecules, the nanoscale entities that make up molecular compounds. Covalent bonds are the result of the net attractive forces that exist when electrons are localized between nuclei. The figure below shows the situation for the simplest possible molecule, H2+, compared with the one-electron atom.
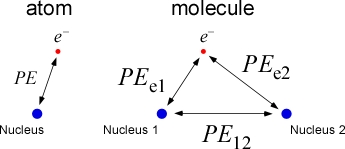
In the molecule, there are three particles: two protons (the nuclei) and an election, which behaves like a wave. There are three electrostatic potential energy terms to consider. The two terms, PEe1 and PEe2 are attractive (sign negative) terms resulting from the attraction between the electron and nucleus 1, and between the electron and nucleus 2, respectively. The term PE12 is a repulsive energy term due to the like-charged nuclei. For the one-electron atom, there is only one electrostatic potential energy term.
When electrons occupy a region of space between two nuclei, they contribute to electrostatic forces that tend to hold nuclei together.
Now, if we introduce a second electron to also occupy a similar space concentrated close between the two nuclei, there will be additional potential energy terms. In particular, an electron-electron repulsion would raise energy, weakening the bond. But at the same time there are the two attractive terms. The net effect is a further lowering of energy, strengthening the bond. The covalent bond is most often characterized as a shared pair of electrons. Why not add a third? One reason is that a theory of bonding making use of molecular orbitals, by analogy with atomic orbitals, requires that at most two electrons can occupy the same orbital. A single covalent bond between atoms can be conceived of as two electrons filling a bonding molecular orbital. We will see that more than one covalent bond may form between two atoms, but additional covalent bonds must arise from electron pairs occupying different bonding molecular orbitals featuring a different spatial distribution of electron probability with respect to the two nuclei.
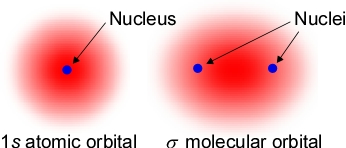
The figure at left illustrates this idea, with the molecular orbital (MO) representing a spatial probability distribution surrounding the two bonded nuclei for an occupying electron. From electrostatic considerations, a molecular orbital for which the electronic probability density is concentrated in the region between the nuclei should contribute to lowering the energy of the molecule compared to the separated atoms. Just this kind of concentration of electron density between the bonded nuclei occurs when two hydrogen atoms with single electrons in their 1s orbitals approach close enough so that there is substantial in-phase overlap between high probability regions of the 1s orbitals.
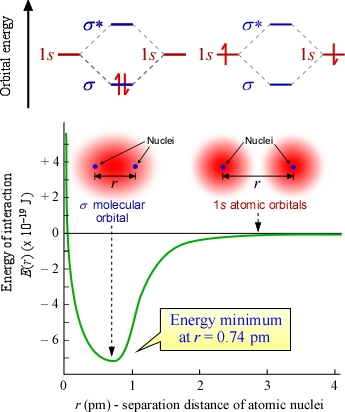
In the figure at right are two different representations of the formation of the diatomic H2 molecule from two hydrogen atoms. The upper orbital energy level diagram shows the electron configuration for H2 on the left and two separate hydrogen atoms on the right. The diagram depicts the molecular orbital theory concept that the two atomic orbitals combine to give rise to two molecular orbitals, σ and σ*, when the atoms approach one another so that the atomic orbitals effectively overlap. The σ orbital is a bonding orbital, and the energy of the H2 molecule is lowered compared to two unbonded hydrogen atoms since the energy level of σ is less that that of 1s. The σ orbital is formed by in-phase addition of the 1s atomic orbitals (recall that orbitals are wave functions), while σ* is an antibonding orbital formed by out-of-phase combination. It is antibonding because in its electron probability distribution the electron probability density is reduced in the region between the nuclei - in fact, there is a nodal plane perpendicular to and bisecting the bond axis. But since both electrons from the H atoms can be accomodated in the σ bonding orbital, the σ* orbital is not occupied in the ground state of the H2 molecule. In other words, MO theory predicts that H2 is a stable molecule. It also predicts that the diatomic helium (He2) molecule is not stable, since the four electrons from two He atoms would have to occupy both the σ and the σ* orbitals so that He2 has no energetic favorability relative to the separated atoms.
In the lower part of the figure the graph depicts the energy of interaction between two initially separate H atoms as the distance between nuclei r decreases from right to left. As r decrease, the energy drops as the atomic orbitals begin to coalesce to form molecular orbitals. The images above the graph represent these orbitals above the corresponding regions of the graph. Eventually a minimum energy is reached, thereafter further reduction in r causes energy to increase dramaically, principally due to electrostatic repulsion between the nuclei. Again, the figure illustrates the lower energy attainable by the formation of the H2 molecule.
The decreased energy of the H2 molecule relative to two separate H atoms is a first illustration of what is termed bond energy, which we can view either as the exothermic energy change associated with formation of the covalent bond from two separate atoms, or as the energetic cost (endothermic eergy change) of breaking the molecule apart into two separate atoms. The energy diagram above for hydrogen shows an energy minimum of 7.24 × 10−19 J, which means that the energy of H2 is that much lower than two separate hydrogen atoms. If we put this on a molar basis (energy of formation of a mole of hydrogen molecules), we have a quantity that is the typical, macroscale units given for bond energies. Multiplying the above quantity by the Avogadro constant, and converting J to kJ,
(7.24 × 10−19 J)(6.022 × 1023 mol−1)(10−3 kJ/J) = 436 kJ/mol
which is the energy in kJ released per mol of H2 molecules formed, or the energy in kJ required per mol of covalent bonds of H2 molecules broken to yield H atoms. We can write these opposing processes as chemical equations, along with their corresponding energy changes (these are called themochemical equations) as follows:
2 H(g) → H2(g) −436 kJ/mol
H2(g) → 2 H(g) +436 kJ/mol
It is important to understand the sign conventions for energy changes for exothermic (negative) and endothermic (positive) processes and to associate a bond energy given as a positive value as a bond breaking process, and to associate bond formation with an energy change that has a negative sign. Keep in mind the following general rules for bond energies:
The formation of a covalent bond is exothermic (energy is released)
The breaking of a covalent bond is endothermic (energy is absorbed)
In other words, the input of energy is required to break a covalent bond, while bond formation releases energy.
Covalent compounds and molecules
Covalent bonds are a feature of molecular compounds, which form from nonmetals. Examples are all the simple homodiatomic molecules in addition to H2: N2, O2 and the halogens F2, Cl2, Br2, and I2. Binary compounds of nonmetals that are simple triatomic molecules include water, carbon dioxide, and several oxides of nitrogen and sulfur.
We would like to explain many of the properties of the substances we observe directly in terms of the nature of the molecules that make them up on the nanoscale. Even though water, hydrogen gas, and oxygen gas are all simple covalent compounds, the chemical difference between the stable elemental forms of the constituents of water - H2(g) and O2(g) - and water (H2O) itself is quite stark.
Ionic vs. covalent bonds
Ionic and covalent character are opposing sides of a spectrum. It is helpful to think of chemical bonding as a continuum, with polar covalent bonding occurring between atoms of moderately different electronegativity, and ionic compounds forming between atoms with the largest differences in electronegativity.