GENERAL CHEMISTRY TOPICS
Density
Density and the units of measurement. Density as a conversion factor. Density and the reliability of measurement.
We define the derived quantity density and discuss it as an illustration of the difference between intensive and extensive properties, its interpretation as a conversion factor, the determination of density by measurement of mass and volume, reliability of measurement, experimental error, and the treatment of significant figures in measurement and calculation.
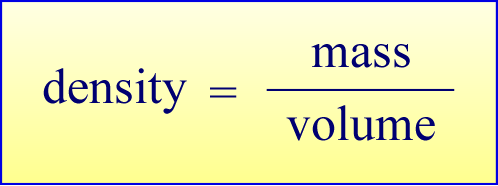
The definition of density is as the ratio of the mass of a substance divided by the volume that mass occupies. The mass and the volume are extensive quantities. These are quantities the values of which depend on the amount of substance present. Since in view of atomic theory all substances are made up of atoms, extensive properties scale with the total number of atoms, or chemical amount. The ratio of these two extensive quantities gives rise to a property - density - that turns out to be independent of chemical amount. For pure, homogeneous substances, density is a characteristic physical property of a substance. A quantity that is independent of amount of substance is termed an intensive quantity.
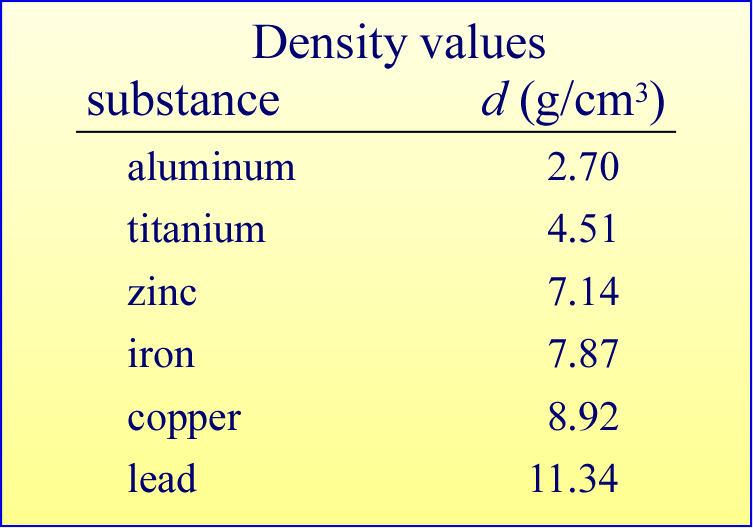
As we can see in the table showing the densities of selected metals, solid substances have a range of density values (unless specified otherwise, these values will be assumed to be for substances at room temperature, or about 20 °C). This range of values suggests that density is a useful property by which we could distinguish different substances. For example, a measurement of density could distinguish between pure gold and an impure sample with gold alloyed with another metal.
By virtue of its definition, density can be viewed as a conversion factor between the mass of a sample of substance and the volume it occupies. If the volume of a sample is measured, its mass can be computed as the product of volume and density. Conversely, the product of the mass of a sample and the inverse of density (termed specific volume) yields the volume of the sample. This is particularly useful in cases where the mass of a sample of substance with a known density can be readily measured, but direct measurements of volume are difficult.
Example: A golden crown has a mass of 745 g. Because of its irregular shape, its volume must be determined by displacement of water. If the crown is indeed made of pure gold (d = 19.3 g/cm3), what volume of water is displaced when the crown is fully immersed?
Solution: Use the inverse of density (i.e. specific volume) as a direct conversion from mass to volume:
V = (1/d) × m
V = (1/19.3 g/cm3) × 745 g = (0.05181347... cm3/g)(745 g) = 38.6 cm3
The volume is reported to three significant figures.