BIOCHEMISTRY TOPICS
Enzyme kinetics
Catalysis and enzymes. Reaction coordinate diagrams, mechanistic models, rate constants and kinetic parameters.
The study of biological catalysis and enzymes is something near and dear to many biochemists. We look at how the principles of chemical kinetics apply to catalysts, including enzymes. We'll find we can construct a simple mechanism for an enzyme-catalyzed reaction.
Catalysis and enzymes
Catalysts are notable for their ability to greatly speed up a reaction despite being in many cases present in substoichiometric amounts. Some of the important features of catalysts are summarized below:
¶ Catalysts speed up reaction rates and are not reactants or products of the net reaction
Catalysts can be participants in a reaction mechanism, combine with reactants to form intermediates, but free catalyst is regenerated, which can then undergo another round of catalysis.
¶ The catalyst provides an alternate mechanism for the reaction, one with a lower activation energy ( kcat > kuncat)
This relates primarily - again - to the participation of the catalyst. A catalyst can speed a bimolecular reaction by bringing the reacting molecules together - providing adjacent, properly-oriented binding sites for the reactants, for example - but it may also provide a completely different mechanistic pathway by reacting to form intermediates that are not accessible in an uncatalyzed mechanism. The lowered activation energy achieved by a mechanism including intermediates reached via lower-energy transition states shows up as a much higher rate constant for the catalyzed reaction: kcat > kuncat.
¶ The position of equilibrium is not affected, but the approach to equilibrium is more rapid
This is a thermodynamic principle. Catalysts do not affect the thermodynamics of a reaction, which determine the equilibrium constant ("Big K") for the reaction. Catalysts affect the reaction kinetics by increasing the rates (little k's) for both the forward and reverse reactions.
¶ Enzymes are biological catalysts and are most commonly protein molecules adapted to speed up a specific reaction
Enzymes are amazing from the standpoint of how greatly they accelerate reaction rates in biological systems, their exquisite specificity (no unintended side products, as in synthetic organic chemistry!), and their ability to do so under mild physiological conditions.
Reaction coordinate diagrams for catalyzed reactions. An explanation for the ability of a catalyst to speed up a reaction is that it can lower the activation energy of the reaction. This can be nicely illustrated using a reaction coordinate diagram.
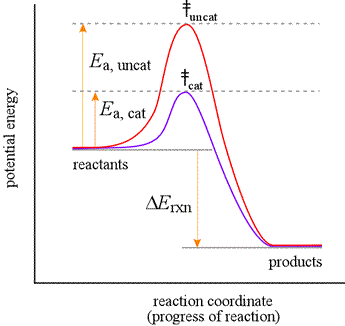
Let us consider the diagram at left to represent an elementary reaction that can take place with or without catalysis. The red curve shows the energy profile for the uncatalyzed reaction. The activation energy for uncatalyzed conversion to products is much greater than that for the catalyzed reaction (indigo curve). This means that the rate constant for the catalyzed reaction, kcat, will be much greater than kuncat, the rate constant for the uncatalyzed reaction. For both the uncatalyzed and the catalyzed reaction, the potential energy change, ΔErxn, is the same. This means that while a catalyst does not alter the conditions under which the reaction is at equilibrium, it greatly speeds up the approach to equilibrium. The reaction coordinate diagram shows that the energy of activation for the reverse reaction is lowered by the catalyst as well.
Enzymatic catalysis
The ability of enzymes to catalyze reactions depends on their ability to interact directly and specifically with reactants The reactant of an enzyme-catalyzed reaction is termed the substrate. An enzyme forms an enzyme-substrate complex as the initial step of its mechanism. The enzyme provides the chemical context for the bound substrate to have access to a low energy path to formation of products. Consider a reaction, S → P, with S the substrate and P the product. Let us suppose the uncatalyzed reaction occurs by a single-step, unimolecular mechanism, and hence would obey a first-order rate law. The mechanism for the enzyme-catalyzed reaction would consist of at least two steps, the first step being formation of the enzyme-substrate (ES) complex, which is an intermediate.
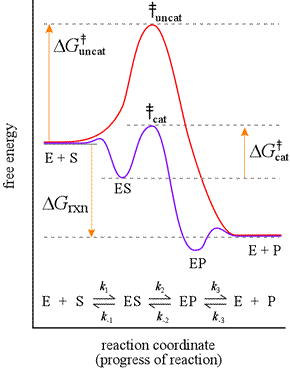
If the formation of the ES complex is thermodynamically favorable, it would be represented on a reaction coordinate diagram at a lower level along the energy axis. The next step, representing the enzyme-bound S-to-P conversion, which we show here as resulting in formation of a enzyme-product (EP) complex, takes place via a much lower energy transition state. A final step to add to this mechanism would be the dissociation of product from the EP complex.
Left: Reaction coordinate diagram for an enzyme-catalyzed reaction representing the mechanistic model we are considering. The free energy of activation, ΔG‡, which for our present purposes can be considered as equivalent to activation energy, is much lower for the catalyzed reaction compared with the uncatalyzed reaction:
ΔG‡cat < ΔG‡uncat
Initial rate vs substrate concentration graph for an enzyme-catalyzed reaction.

The figure at right shows the idealized results of measurements of a typical enzyme-catalyzed reaction. Initial rates are measured at different starting substrate concentrations, and when these are graphed, it is found that the measured values are well-fit by a hyperbolic curve given by the equation shown. Two parameters describe this equation. One parameter is Vmax, which represents a limiting maximum velocity, the rate approached as the substrate concentration increases. The other is usually called KM, which corresponds to the substrate concentration at which V = Vmax /2. The experimental data and the rate vs. substrate equation indicate a zero-order reaction when substrate concentration becomes much greater than KM, while when substrate concentration is low ([S] << KM), the rate is that of a first-order reaction, with V0 = (Vmax / KM ) [S].
A simplified mechanism for an enzyme-catalyzed reaction.
It is possible to write a much-simplified mechanism for an enzyme-catalyzed reaction, and employ it to predict the hyperbolic dependence of the initial reaction rate on substrate concentration. The first step of this mechanism is formation of the ES complex, since in order for an enzyme to catalyze the reaction, the enzyme E must form a complex with the substrate. In the second step of the mechanism, the ES complex directly yields free enzyme and free product:
(1) E + S → ES (substrate binding step)
(2) ES → E + P (catalytic step)
The enzyme-substrate complex, ES, is thus the intermediate in the mechanism. In the ES complex, the enzyme binds substrate in a way that creates a low-activation energy path for its conversion to product. Here, what may in reality be several distinct mechanistic steps leading from ES to products are collapsed to a single catalytic step.
Mechanism-based prediction of hyperbolic dependence of rate on substrate concentration
Does such a simple mechanism explain experimental observations of enzyme-catalyzed reactions (i.e. the typical initial velocity vs. substrate concentration curve as illustrated above)? Yes, and one way to show that this is the case is to make the assumption that step (1), formation of the ES complex, is significantly faster than step (2), production of products from ES, i.e. the mechanism can be represented as
(1) E + S = ES (fast)
(2) ES → E + P (slow)
This is not true for all enzymes, but it is true enough for some, and those cases where this assumption does not hold can be dealt with using an alternate assumption that leads ultimately to the same result. Now if step (2) is the much slower step, it is the rate-limiting step, and its rate determines the overall reaction rate. Writing the rate law for this elementary step, we have
V0 = k2 [ES]
where V0 is observed initial rate of reaction, and k2 is the first-order rate constant for step (2) in the forward direction. Since ES is an intermediate and the rate law for a reaction is expressed in terms of a rate constant and reactant concentrations, we must find an expression for [ES] in terms of [S] (strictly speaking, we mean [S]0, the initial substrate concentration). In this case, we will also make use of the total enzyme concentration, [E]T, since this is a quantity that we can control in the experimental setting. We can see that at high substrate concentrations, essentially all enzyme at any instant has substrate bound, and therefore [ES] = [E]T, and the enzyme is being driven as fast as it can possibly go, given its limited amount. Under such conditions, we say that the enzyme is saturated with substrate, and we have
Vmax = k2 [E]T
The parameter Vmax is thus set by the catalytic rate constant and total enzyme concentration. To get [ES] at less than saturating substrate concentrations, we use both the relation [ES] = [E]T – [E], where [E] is the concentration of free enzyme, and the relation we get from assuming that step (1) is at equilibrium:
k1/ k–1 = [ES] / [E][S]
where k1 and k–1 are the forward and reverse rate constants, respectively, for step (1). Solving the latter for [E] and substituting into the above expression for [ES], we obtain
[ES] = [E]T – [E] = [E]T – (k–1/ k1)( [ES] / [S] )
Solving this for [ES], we have
[ES] = [E]T – [E] = [E]T /{(k–1/k1)(1 / [S]) + 1} = [E]T [S] /{(k–1/k1) + [S]}
If we now define KM = k–1/k1 (i.e. KM is the equilibrium constant for the dissociation of the ES complex to free enzyme and unbound substrate, the equation for which is the reverse of step 1, ES = E + S) and combine the expression for [ES] we just obtained with the rate equation V0 = k2 [ES], we have
V0 = k2 [ES] = k2[E]T [S] /{KM + [S]} = Vmax [S] /{KM + [S]}
where we have substituted Vmax = k2 [E]T to obtain the last equality, which gives us the equation we were after. This shows that the simple mechanism we proposed above as a model for at least some enzyme-catalyzed reactions does indeed give us an initial rate vs. substrate concentration curve consistent with what is typically observed in enzyme kinetics experiments. This equation is known as the Michaelis-Menten equation. Note that at very high [S] ([S] >> KM), KM becomes insignificant compared to [S] in the denominator of the Michaelis-Menten equation, which becomes approximated as
V0 ≈ Vmax [S] / [S] = Vmax
which represents saturation of the enzyme with substrate ([ES] ≈ [E]T). On the other hand, when substrate concentration is very low ([S] << KM), KM becomes insignificant compared to [S] in the denominator of the Michaelis-Menten equation, which the becomes approximated as
V0 ≈ (Vmax / KM ) [S]
where Vmax / KM represents a pseudo-first order rate constant. In addition, setting substrate concentration equal to KM yields V0 = ½Vmax.