GENERAL CHEMISTRY TOPICS
Energy: Foundational concepts
Forms of energy: Kinetic and potential. Work and energy. Heat and temperature. Electrostatic potential energy.
Energy: kinetic and potential
The concept of energy is fundamental to the physical sciences. Here we aim to set forth some first principles regarding energy, and to introduce some of the forms that energy takes that are of particular importance to chemistry. First of all, it is often very useful to define a system to mean a particular part of the universe upon which our observations are made. The system is made up of an object or collection of objects, and is distinguished from the rest of the universe - which we call the surroundings - by a real or imaginary boundary.
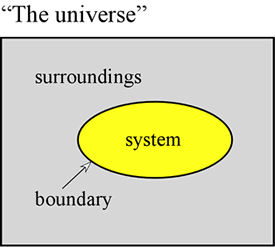
A sample of gas held within a fixed volume, such as a metal cylinder, is an example of a system - one that will be of relevance to us when we take up the study of general properties of gases. Further examples are a sample of gas inside a balloon or a combustion mixture in a cylinder with a piston. In both these cases the system is enclosed by a physical, but movable boundary, so that the volume of the system is not fixed. An additional example that we will often consider is that of a mixture of substances in solution undergoing a chemical reaction within a test tube or beaker. The terminology introduced here is of particular importance in the study of how energy manifests in chemical systems, which falls largely under the heading of thermodynamics.
In general chemistry, the systems we consider as relevant are typically at rest and gravitational effects are ignored. Often, we are most interested in systems within which chemical reactions take place, the chemical composition of the system changing with time. Let us for the moment, however, adopt a broader perspective by using mechanical systems such as a swinging pendulum, or billiard balls rolling and colliding, to help us understand general principles relating to energy.
A system can be said to possess energy in two different ways, which we call kinetic and potential energy. Kinetic energy is the energy of matter in motion. Physics provides an exact mathematical definition of kinetic energy (KE), shown in the equation (below left).

Here, the kinetic energy of an object is represented as a product of the object's mass (m) and the square of its velocity (v), multiplied also by the constant ½. If the system consists of more than one object, the total kinetic energy is expressible as a sum of the kinetic energies of the individual objects.
We can derive units for energy given this definition. The SI unit for energy is the joule (J), which is defined as:
1 J = 1 kg·m·s−2
Potential energy is the energy of a system that can typically be converted to kinetic energy in some form, and able to produce, in some measure, a quantity called work (discussed further below). A clear example of potential energy is a brick on the ledge of a building. The brick has a certain amount of potential energy by virtue of its height - its location with respect to a gravitational field. If we give the brick a nudge, so that it falls off the ledge, it spontaneously moves in the direction of lower gravitational potential energy, and as it does so it gains kinetic energy. Another example is the electric potential energy of a battery (which is expressed in terms of voltage). When a circuit is made with a wire and a light bulb, connecting the two terminals of a battery, the difference in electric potential between them cause electrons in the wire to move (kinetic energy), resulting in the production of both heat and light.
An important general principle about energy is that it can be neither created nor destroyed. This is known as the law of conservation of energy. Quantitatively, this means that in a system such as the falling brick or a clock's pendulum, the sum of kinetic and potential energy is constant. This is somewhat of an abstraction, since in a real pendulum, some of the energy is continually being lost due to friction, and a small amount of energy must be added to the pendulum to keep it swinging (and the clock working). But if we account for such "lost" energy (which actually appears as an increase in the heat energy of the surrounding air molecules) by careful experimental measurements, it is found that indeed energy is always conserved. Another caveat is summarized in Einstein's famous equation E = mc2, which expresses a fundamental equivalence of mass and energy. A more general form of the law of conservation of energy, which can be termed the law of conservation of mass-energy, accounts for this equivalence. Returning to general chemistry, such matter-energy interconversions are not typically its province, whereas the study of nuclear reactions and radioactivity is encompassed by nuclear physics.
If we consider a chemical reaction in which chemical changes are accompanied by the production of heat, a question arises: What about conservation of energy in this case? The answer is that there is a form of potential energy, which we can call chemical potential energy (or simply chemical potential), that can be thought of as residing in the molecular composition of the reactants. This potential energy is then converted to energy in the form of heat, but it turns out that the net amount of energy present remains constant, once we are able to define and measure the production of heat. An everyday example of what we can now understand as chemical potential energy is given by a gasoline engine, wherein the mixture of gasoline and oxygen possesses a latent form of energy. This latent energy in the gasoline/oxygen mixture is expended to produce the kinetic energy of a car.
Work and energy
Work is another concept that admits a precise definition in physics. Furthermore, the laws of mechanics can be tied in with energy by means of the work-energy theorem. A kick of a soccer ball or any number of similar examples illustrate the idea that the kinetic energy of an object can be increased by application of a force. The work-energy theorem, which is a generalization of this idea, can be stated roughly as follows: The change in the energy an object possesses is equal to the magnitude of the force acting on it, multiplied by the distance through which the force acts.
The energy change occurring in a system as a result of work can be positive or negative, from the point of view of the system. Work can be done by a system, or a system can have work done upon it by the surroundings. If work is done by a system, it loses energy to the surroundings. If the system has work done upon it, the energy of the system is increased. For example, when a spark setting off a combustion mixture in a cylinder with a movable piston causes a rapid expansion of the system, and the expansion is mechanically coupled to the motion of a rod or flywheel in the surroundings, the system of the cylinder does work on the surroundings, and in so doing, loses energy. This of course is a part of how an internal combustion engine converts chemical potential energy into the kinetic energy of a car in motion.
One implication of the work-energy theorem is for units, namely that work can be measured in the same units as energy. Since Newton's second law is force = mass × acceleration, the newton (N), the SI unit for force, is derived as M × L × T −2, and thus 1 N = 1 kg m s−2. Force times distance has quantities M × L2 × T −2, and so the SI unit for energy, the joule (J), is defined as 1 J = 1 kg m2 s−2. At this point, you should verify for yourself that the equation for kinetic energy involves the same combination of the fundamental quantities mass (M), length (or distance, L) , and time (T).
Heat and temperature
We use the words heat and temperature quite frequently, and often speak of heat as a form of energy. We all have an intuitive sense of what these things are, but here we want to think about them more scientifically, and give them more formal definitions if we can. This is a necessary prelude to the quantification of the energy corresponding to heat, and thence to measurements to verify the law of conservation of energy. What we find is that the heat energy of a system may be likened to the total kinetic energy (as defined above) of the atoms and molecules that compose it. The temperature of an object or system is actually a measure of the average kinetic energy of the constituent atoms and/or molecules. (N.B. Temperature is not exactly equal to the average molecular kinetic energy, but is directly proportional to it. For further details, see the kinetic molecular theory web page.)
One way to visualize what we mean by heat and temperature, and the distinction between them, is to consider a billiard ball analogy. In some simple contexts, the behavior of billiard balls are an adequate model for a collection of atoms or molecules, such as in a sample of a gas. Just like billiard balls that have been just struck by a rapidly moving cue ball, the molecules of a gas are moving all about, bouncing off each other and the walls of the container holding them. The total kinetic energy of the billiard balls, which is just the sum of the individual kinetic energies of each ball, is analogous to the thermal energy content of a sample of gas molecules. In a "break" at the start of a game of billiards, the initial kinetic energy of the cue ball is distributed among all the balls on the table. Some are moving quite fast, and others not so fast, but the analogy to "heat" or "thermal energy" for the system of billiard balls is just the sum of these kinetic energies. On the other hand, the temperature of the billiard ball system would be proportional to the average kinetic energy of the ensemble of balls.
Electrostatic potential energy
The law of electrostatic attraction and repulsion, or Coulomb's Law, describes the force exerted on a charged object due to the presence of another charged object. The force is most easily calculated when the charges can be treated as very small point charges. The magnitude of force a charged object "feels" is proportional to the product of the charges (the SI unit for electric charge is the Coulomb, C), and inversely proportional to the square of the distance of separation between the charges (r in the figure at right). The force is an attractive force (like gravity, and indicated by inward-pointing arrowheads in the figure) if the charges are opposite in sign, and repulsive when the charges have the same sign.
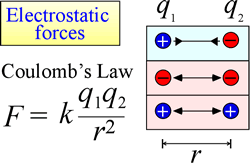
When force (such as electrostatic, magnetic, and gravitational forces) can act at a distance (through space, without mechanical contact), the objects subject to such forces are said to be in a potential energy field. We spoke of gravitational potential energy above, and similarly in the case of electrostatic forces, a charged object will have electrostatic potential energy by virtue of its location in an electric field. Such a field exists in the vicinity of any other charge or charges.
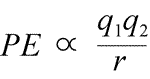
Equation for electrostatic potential energy: PE is proportional to charges q1 and q2, and inversely proportional to separation distance, r. The form of the potential energy function follows mathematically from the force expression, Coulomb's Law.
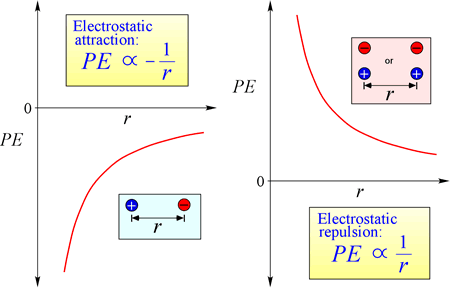
Given the opposing signs of charges in attraction, the potential energy is always negative, and the closer the charges approach, the more negative - i.e. the lower - potential energy becomes. As the separation distance, r approaches zero, potential energy becomes infinitely negative. For charges of the same sign, the energy of repulsion is always positive, and becomes infinitely positive as the separation distance, r approaches zero.
Electrostatic potential energy is an important consideration in chemistry. An understanding of the nature of the atom, chemical bonding, and intermolecular forces are all absolutely dependent on accounting for the influence of charge-charge interactions that contribute to the energy of a system.
Important units
Energy (SI unit) 1 joule = 1 J = 1 kg·m·s−2
Elementary charge, e = 1.60218 × 10−19 C (coulomb, C)
Faraday constant: F = NAe = 9.64853 × 104 C·mol−1
Electric potential: volts, V 1 V = 1 J C−1